Question

In an amusement-park ride, riders stand with their backs against the wall of a spinning vertical cylinder. The floor falls away and the riders are held up by friction. The acceleration of gravity is 9.81 m/s 2 . If the radius of the cylinder is 3 m, find the minimum number of revolutions per minute necessary when the coefficient of static friction between a rider and the wall is 0.7. Answer in units of rev/min

Answer 1

90.78 rev/min

Step-by-step explanation:

In first place, we have to do the force balance to determine the minimum angular speed required to avoid slipping. The forces acting here are friction and the force due to circular movement, that is centripetal force. Then, we have:

`f=ma_(c)`

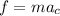
μmg=mRω^2

ω=
`\sqrt{(μg)/(R) } \\`

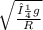
Then, replacing the given values in the expression we have the following result:

ω=1.51 rev/s*60s=90.78 rev/min