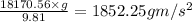Question

The propeller of a World War II fighter plane is 2.30 m in diameter. (a) What is its angular velocity in radians per second if it spins at 1200 rev/min? (b) What is the linear speed of its tip at this angular velocity if the plane is stationary on the tarmac? (c) What is the centripetal acceleration of the propeller tip under these conditions? Calculate it in meters per second squared and convert to multiples of g .

Answer 1

Answer with Explanation:

We are given that

Diameter of fighter plane=2.3 m

Radius=
`r=(d)/(2)=(2.3)/(2)=1.15 m`

a.We have to find the angular velocity in radians per second if it spins=1200 rev/min

Frequency=
`(1200)/(60)=20 Hz`

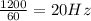
1 minute=60 seconds

Angular velocity=
`\omega=2\pi f`

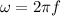
Angular velocity=
`2* (22)/(7)* 20=125.7 rad/s`

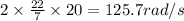
b.We have to find the linear speed of its tip at this angular velocity if the plane is stationary on the tarmac.

`v=r\omega=1.15* 125.7=144.56 m/s`

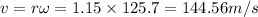
c.Centripetal acceleration=
`\omega^2 r=(125.7)^2(1.15)=18170.56 m/s^2`

Centripetal acceleration==
`(18170.56* g)/(9.81)=1852.25 g m/s^2`