Step-by-step explanation:
It is given that,
Mass of Adolf,
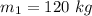
Mass of Ed,
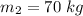
Adolf swings upward to a height of 0.52 m above his starting point. Initially both men are at rest. Their momentum will remain conserved.
Firstly, finding the speed of Adolf by using the conservation of energy as :

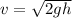
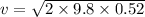
v = 3.19 m/s
Let v' is the speed of Ed. It can be calculated using the conservation of momentum as :
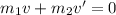
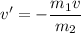
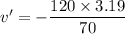
v' = -5.46 m/s
Let H is the height above which Ed rise. It can be calculated using the conservation of energy again as:
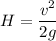
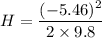
H = 1.52 meters
So, Ed will rise to a height of 1.52 meters. Hence, this is the required solution.