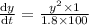Question

A floodlight at ground level is illuminating a building that is 100m away. A man 1.8m tall is walking from the floodlight to the building along a path that is perpendicular to the building. If he is walking at the rate of 1m/s, at what rate is his shadow on the building decreasing when he is 60 m from the building Expert Answer

Answer 1

Answer:0.1125 m/s

Step-by-step explanation:

Given

Height of Person is 1.8 m

walking rate towards building is 1 m/s

From Similar triangle concept

`(40)/(100)=(1.8)/(y)`

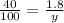
y=4.5 m

Now suppose at any distance x between man and building

`(100-x)/(100)=(1.8)/(y)`

`1-(x)/(100)=(1.8)/(y)`

Differentiate w.r.t to time

`-\frac{\mathrm{d} x}{\mathrm{d} t}=-(1.8)/(y^2)\frac{\mathrm{d} y}{\mathrm{d} t}`

and
`\frac{\mathrm{d} x}{\mathrm{d} t}=1 m/s`

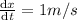
and at x=60 y=4.5 m

`\frac{\mathrm{d} y}{\mathrm{d} t}=(y^2* 1)/(1.8* 100)`

`\frac{\mathrm{d} y}{\mathrm{d} t}=0.1125 m/s`