Answer:
Acceleration is
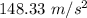
Solution:
As per the question:
Radius of the circle, R = 1.8 m
Height above the ground, h = 1.8 m
Horizontal distance, x = 9.9 m
Now,
The magnitude of the centripetal acceleration can be calculated as:
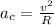
where
v = velocity
R = radius
 = centripetal acceleration
= centripetal acceleration
Now, if we consider the vertical component of motion only, then considering the initial velocity, 'u' = 0, from kinematic eqn:
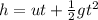
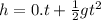

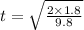
t = 0.606 s
Now, for the horizontal component of velocity:
x = vt
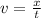
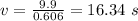
Now, we know that the centripetal acceleration is given by:
