Answer:
0.0498
Explanation:
given,
The time between surface finish problems in a galvanizing process is exponentially distributed with a mean of 42 hours.
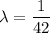
a) probability that none of the lines experiences a surface finish problem in 42 hours of operation
=

=
![((1)/(42))^3\int_(42)^(\infty) \int_(42)^(\infty) \int_(42)^(\infty) (e^{(-x)/(42)})\ (e^{(-y)/(42)})\ [\frac{e^{(-z)/(42)}}{(-1)/(42)}]_(42)^(\infty)dx\ dy\ dz](https://img.qammunity.org/2020/formulas/mathematics/college/vl1l96x0g3el605fhtwyp6dkff58scegly.png)
=
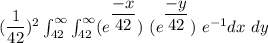
=
![((1)/(42))^2\ e^(-1)[\frac{e^{(-y)/(42)}}{(-1)/(42)}]_(42)^(\infty)](https://img.qammunity.org/2020/formulas/mathematics/college/8y5wuofonwpuljbw9mcskcfmfyd1px8xwl.png)
=
![((1)/(42)) \ e^(-1)\ e^(-1)[\frac{e^{(-x)/(42)}}{(-1)/(42)}]_(42)^(\infty)](https://img.qammunity.org/2020/formulas/mathematics/college/voqu55m4kqols309h6z2ymbkxewbtptijc.png)
=
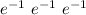
=
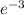
= 0.0498