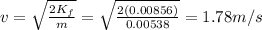Question

A toy cannon uses a spring to project a 5.38-g soft rubber ball. The spring is originally compressed by 5.08 cm and has a force constant of 7.91 N/m. When the cannon is fired, the ball moves 14.5 cm through the horizontal barrel of the cannon, and the barrel exerts a constant friction force of 0.032 3 N on the ball. (a) With what speed does the projectile leave the barrel of the cannon? m/s (b) At what point does the ball have maximum speed? cm (from its original position) (c) What is this maximum speed? m/s

Answer 1

(a) 1.43 m/s

We can solve this problem by using the law of conservation of energy.

The initial total energy stored in the spring-mass system is

`E=U=(1)/(2)kx^2`

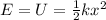
where

k = 7.91 N/m is the spring constant

`x=5.08 cm = 0.0508 m`

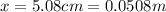
Substituting,

`E=(1)/(2)(7.91)(0.0508)^2=0.0102 J`

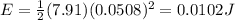
The final kinetic energy of the ball is equal to the energy released by the spring + the work done by friction:

`E+W_f=K`

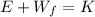
where

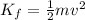`K_f=(1)/(2)mv^2` is the kinetic energy of the ball, with

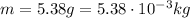`m=5.38 g = 5.38\cdot 10^(-3) kg` being the mass of the ball

v being the final speed

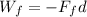`W_f = -F_f d` is the work done by friction (which is negative since the force of friction is opposite to the motion), where

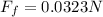`F_f = 0.0323 N` is force of friction

d = 14.5 cm = 0.145 m is the displacement

Substituting,

`W_f = -(0.0323)(0.145)=-4.68\cdot 10^(-3) J`

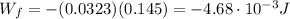
So, the kinetic energy of the ball as it leaves the cannon is

`K_f = E+W_f = 0.0102 - 4.68\cdot 10^(-3)=0.00552 J`

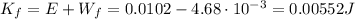
And so the final speed is

`v=\sqrt{(2K_f)/(m)}=\sqrt{(2(0.00552))/(0.00538)}=1.43 m/s`

(b) +5.08 cm

The speed of the ball is maximum at the instant when all the elastic potential energy stored in the spring has been released: in fact, after that moment, the spring does no longer release any more energy, so the kinetic energy of the ball from that moment will start to decrease, due to the effect of the work done by friction.

The elastic potential energy of the spring is

`U=(1)/(2)kx^2`

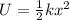
And this has all been released when it becomes zero, so when x = 0 (equilibrium position of the spring). However, the spring was initially compressed by 5.08 cm, so the ball has maximum speed when

x = +5.08 cm

with respect to the initial point.

(c) 1.78 m/s

The maximum speed is the speed of the ball at the moment when the kinetic energy is maximum, i.e. when all the elastic potential energy has been released.

As we calculated in part (a), the total energy released by the spring is

E = 0.0102 J

The work done by friction here is just the work done to cover the distance of

d = 5.08 cm = 0.0508 m

Therefore

`W_f = -(0.0323)(0.0508)=-1.64\cdot 10^(-3) J`

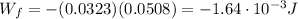
So, the kinetic energy of the ball at the point of maximum speed is

`K_f = E+W_f = 0.0102 - 1.64\cdot 10^(-3)=0.00856 J`

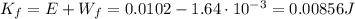
And so the final speed is

`v=\sqrt{(2K_f)/(m)}=\sqrt{(2(0.00856))/(0.00538)}=1.78 m/s`