Question

A bucket is 20cm in diameter at the top, and 14cm in diameter at the bottom and 15cm deep.

Calculate the:
A. Capacity of the bucket in litres
B. Curved surface area of the bucket

Answer 1

A ) Capacity of the bucket = 3.441 liters

B ) Curved surface area of the bucket = 53.38 cm²

Explanation:

Given in question as,

Diameter (D) of top of bucket = 20 cm , So Radius ( R ) =
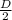`(D)/(2)` = 10 cm

Diameter (d) of bottom of bucket = 14 cm , So r =
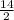`(14)/(2)` = 7 cm

Depth of bucket = 15 cm

So, from given values it is clear that bucket shape is of FRUSTUM

A ) From the above data , the volume of frustum is calculated

So,Volume of frustum =
`(1)/(3)` ×
`\pi` × h ×( R² + r² +R ×r )

i,e Volume =
`(1)/(3)` ×
`\pi` × 15 ×( 10² + 7² + 10×7 )

So, Volume =
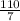`(110)/(7)` × 219 = 3441.42 cm³ = 3.441 liters

Now covert this value in liters

∵ 1 cm³ = 0.001 liter

So, 3441042 cm³ = 3.441 liters

B) Curved surface Area =
`\pi` (R + r)

CSA =
`\pi` ( 10 + 7)

CSA = 3.14 × 17 = 53.38 cm²

Hence The capacity of frustum is 3.441 liters and The curved surface area = 53.38 cm² Answer