Answer:
 or
or

Explanation:
You need to complete the square before you can take the square root of both sides.

Subtract 10 from both sides.
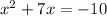
To complete the square, you need to add the square of half of the x-term coefficient to both sides.
The x-term coefficient is 7. Half of that is 7/2. Square it to get 49/4. Now we add 49/4 to both sides of the equation.
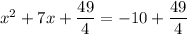
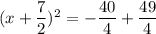
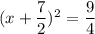
Now we use the square root property, if
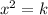 , then
, then

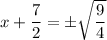
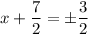
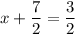 or
or
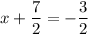
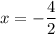 or
or
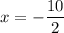
 or
or
