Question

Consider the brass alloy for which the stress-strain behavior is shown in the Animated Figure 7.12. A cylindrical specimen of this material 10.0 mm (0.3937 in.) in diameter and 100.6 mm (3.961 in.) long is pulled in tension with a force of 9970 N (2241 lbf). If it is known that this alloy has a value for Poisson's ratio of 0.35, compute

(a) the specimen elongation,
(b) the reduction in specimen diameter.

because the diameter decreases, enter a minus sign in your answer.

Answer 1

(a) 0.1509 mm

(b) 0.00525 mm

Step-by-step explanation:

Stress,
`\sigma` is given by

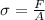`\sigma=\frac {F}{A}` where F is force and A is area and area is given by
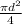`\frac {\pi d^(2)}{4}` hence

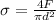`\sigma=\frac {4F}{\pi d^(2)}` where d is the diameter. Substituting 9970 N for F and 10mm=0.01 m for d hence

`\sigma=\frac {4*9970 N}{\pi 0.01m^(2)}=126941982.6 N/m^(2)`

`\sigma \approx 127 Mpa`

From the attached stress-strain diagram, the stress of 127 Mpa corresponds to strain of 0.0015 and since strain is given by

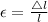`\epsilon=\frac {\triangle l}{l}` where
`\epsilon` is the strain,
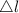`\triangle l` is elongation and l is original length and making elongation the subject

`\triangle l= \epsilon * l` and substituting strain with 0.0015 and length l with 100.6 mm then

`\triangle l=0.0015* 100.6=0.1509 mm`

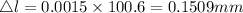
(b)

Lateral strain is given by

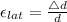`\epsilon_(lat)=\frac {\triangle d}{d}` and substituting
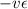`-v\epsilon` for
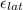`\epsilon_(lat)` where v is poisson ratio then

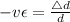`-v\epsilon=\frac {\triangle d}{d}` and making
`\triangle d` the subject then

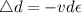`\triangle d=-vd\epsilon` and substituting 0.35 for v, 0.0015 for strain and 10 mm for d

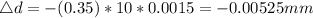`\triangle d=-(0.35)*10*0.0015=-0.00525 mm` and the negative sign indicates decrease in diameter