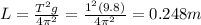Answer:
0.248 m
Step-by-step explanation:
The period of a simple pendulum is given by

where
L is the length of the pendulum
g is the acceleration of gravity
The pendulum in the problem passes its lowest point twice every second: this means: this means that it makes one complete oscillation in one second, so its period is 1 second:
T = 1 s
And using

We can rearrange the equation above to find L, the length of the pendulum: