For this case we find the slopes of each of the lines:
The g line passes through the following points:
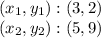
So, the slope is:
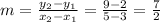
Line h passes through the following points:
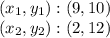
So, the slope is:
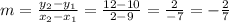
By definition, if two lines are parallel then their slopes are equal. If the lines are perpendicular then the product of their slopes is -1.
It is observed that lines g and h are not parallel. We verify if they are perpendicular:
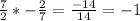
Thus, the lines are perpendicular.
Answer:
The lines are perpendicular.