Answer:
 and
and
 .
.
Explanation:
If we have to different functions like the ones attached, one is a parabolic function and the other is a radical function. To know where
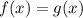 , we just have to equalize them and find the solution for that equation:
, we just have to equalize them and find the solution for that equation:
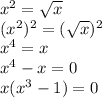
So, applying the zero product property, we have:
![x=0\\x^(3)-1=0\\x^(3)=1\\x=\sqrt[3]{1}=1](https://img.qammunity.org/2020/formulas/mathematics/middle-school/u8dt6n1bzlmo74hby4z13xo0od7zi7k40v.png)
Therefore, these two solutions mean that there are two points where both functions are equal, that is, when
 and
and
 .
.
So, the input values are
 and
and
 .
.