Evaluate A + 3B if possible. HELP ASAP!

Question

asked Feb 25, 2020 8.0k views

2 Answers

Ayyash · Answer 1 · 2020-02-28T00:41:16+0000

Answer: Not possible

Explanation:

Matrix A is a 3 × 2 matrix.

Matrix B is a 2 × 3 matrix.

The scalar product 3B is also a 2 × 3 matrix.

The dimensions of A and 3B are not the same. Therefore, the matrices cannot be added

Challet · Answer 2 · 2020-03-01T00:51:03+0000

Answer:

Not possible.

Explanation:

Addition of Matrix A and Matrix B is possible only if the order of matrix A is same as the order of matrix B.

Order of a matrix with
rows and
columns is
.

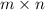Here, matrix A is
$\left[\begin{array}{ccc}2&-4\\-4&10\\0&-8\end{array}\right]$

Matrix B is
$\left[\begin{array}{ccc}0&-4&6\\2&-10&4\end{array}\right]$ .

Multiplying a matrix by a constant doesn't change its order.

So, order of matrix A is
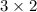3* 2 as it has 3 rows and 2 columns.

The order of matrix 3B is
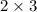2* 3 as it has 2 rows and 3 columns.

Therefore, addition is not possible as the order is different.