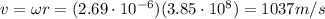Question

Assuming the orbital radius of the Moon is 3.85 x 108 m, find the linear speed of the moon.

Answer 1

1037 m/s

Step-by-step explanation:

The linear speed of an object in circular motion is given by:

`v=\omega r`

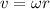
where

`\omega` is the angular velocity

r is the orbital radius

For the Moon, we know that

`r=3.85\cdot 10^8 m` is the orbital radius

While we know also its orbital period:

`T=27 days \cdot (24\cdot 3600)=2.33\cdot 10^6 s`

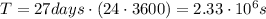
So its angular velocity is

`\omega = (2\pi)/(T)=(2\pi)/(2.33\cdot 10^6)=2.69\cdot 10^(-6) rad/s`

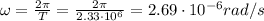
And therefore, the linear speed is

`v=\omega r=(2.69\cdot 10^(-6))(3.85\cdot 10^8)=1037 m/s`