Answer:
a) SPAZ is equilateral.
b) Diagonals SA and PZ are perpendicular to each other.
c) Diagonals SA and PZ bisect each other.
Explanation:
At first we form the triangle with the help of a graphing tool and whose result is attached below. It seems to be a paralellogram.
a) If figure is equilateral, then SP = PA = AZ = ZS:
![SP = \sqrt{[4-(-4)]^(2)+[(-2)-(-4)]^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/zzb86wp0hgo0qrgbmev2hkcpc538ar9p39.png)

![PA = \sqrt{(6-4)^(2)+[6-(-2)]^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/cpti8w4n8dmksfo6mlt7hjhlqng64zmd5p.png)
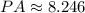
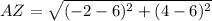
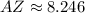
![ZS = \sqrt{[-4-(-2)]^(2)+(-4-4)^(2)}](https://img.qammunity.org/2022/formulas/mathematics/high-school/2ev1jbf402rmuao2gfphv2s0et5gt889mm.png)

Therefore, SPAZ is equilateral.
b) We use the slope formula to determine the inclination of diagonals SA and PZ:
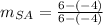
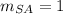
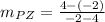
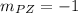
Since
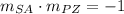 , diagonals SA and PZ are perpendicular to each other.
, diagonals SA and PZ are perpendicular to each other.
c) The diagonals bisect each other if and only if both have the same midpoint. Now we proceed to determine the midpoints of each diagonal:
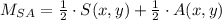
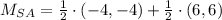

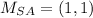
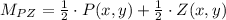
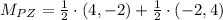
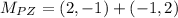
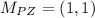
Then, the diagonals SA and PZ bisect each other.