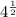Question

Which expression is equivalent to (4 ^5/44 ^1/4/4 ^1/2) ^1/2

Answer 1

C= 2

Explanation:

Answer 2

For this case we must find an expression equivalent to:

`(\frac {4 ^ {\frac {5} {4}} * 4 ^ {\frac {1} {4}}} {4 ^ {\frac {1} {2}}})^{{\frac { 1} {2}}`

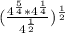
By definition of multiplication of powers of equal base we have that the same base is placed and the exponents are added:

`(\frac {4 ^ {\frac {5 + 1} {4}}} {4 ^ {\frac {1} {2}}}) ^ {\frac {1} {2}} =\\(\frac {4 ^ {\frac {6} {4}}} {4 ^ {\frac {1} {2}}}) ^ {\frac {1} {2}} =\\(\frac {4 ^ {\frac {3} {2}}} {4 ^ {\frac {1} {2}}}) ^ {\frac {1} {2}} =`

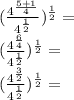
By definition of division of powers of the same base we have that the same base is placed and the exponents are subtracted:

`(4 ^ {\frac {3} {2} - \frac {1} {2}})^{(1)/(2)}`

`(4 ^ {\frac {3-1} {2}})^{{\frac {1} {2}} =`

`(4 ^ {\frac {2} {2}})^{{\frac {1} {2}} =`

`(4^1) ^ {\frac {1} {2}} =`

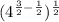
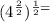
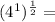
By definition of power properties we have to:

`(a ^ n) ^ m = a ^( n * m)`

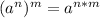
Then, the expression is reduced to:

`4 ^ {\frac {1} {2}}`

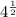
Answer:

`4 ^ {\frac {1} {2}}`