Answer:
Option A.
Explanation:
Note : The given function is linear, all options are incorrect for linear function.
Consider the given function is
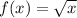
For x=81,
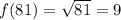
For x=36,
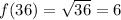
For x=1,
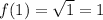
It means the given function passes through the points (81,9), (36,6) and (1,1).
If a graph reflected across y-axis then
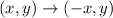
So, the new function is
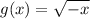
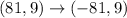
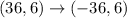
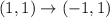
It means points (-81, 9), (-36, 6) and (-1, 1) lie on the graph of the reflection.
Therefore, the correct option is A.