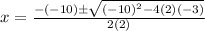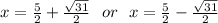Question

What are the zeros of the quadratic function f(x) = 2x2 – 10x – 3? x = StartFraction negative 5 Over 2 EndFraction – StartFraction StartRoot 31 EndRoot Over 2 EndFraction and x = StartFraction negative 5 Over 2 EndFraction + StartFraction StartRoot 31 EndRoot Over 2 EndFraction x = StartFraction negative 5 Over 2 EndFraction – StartFraction StartRoot 37 EndRoot Over 8 EndFraction and x = StartFraction negative 5 Over 2 EndFraction + StartFraction StartRoot 37 EndRoot Over 8 EndFraction x = StartFraction 5 Over 2 EndFraction – StartFraction StartRoot 31 EndRoot Over 2 EndFraction and x = StartFraction 5 Over 2 EndFraction + StartFraction StartRoot 31 EndRoot Over 2 EndFraction x = StartFraction 5 Over 2 EndFraction – StartFraction StartRoot 37 EndRoot Over 8 EndFraction and x = StartFraction 5 Over 2 EndFraction + StartFraction StartRoot 37 EndRoot Over 8 EndFraction

Answer 1

Explanation:

It’s D

Answer 2

`x=(5)/(2)+(√(31))/(2)\ \ or\ \ x=(5)/(2)-(√(31))/(2)`

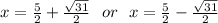
Explanation:

Given the following Quadratic function:

`f(x) = 2x^2 - 10x -3`

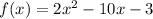
We must make it equal to zero:

`0 = 2x^2 - 10x -3`

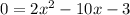
Now we need to apply the Quadratic formula. This is:

`x=(-b\± √(b^2-4ac))/(2a)`

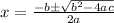
In this case we can identify that:

`a=2\\b=-10\\c=-3`

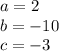
Finally, substituting these values into the Quadratic formula, we get the following solutions:

`x=(-(-10)\±√((-10)^2-4(2)(-3)))/(2(2))`

`x=(5)/(2)+(√(31))/(2)\ \ or\ \ x=(5)/(2)-(√(31))/(2)`