Question

The distribution of the number of transactions performed at a bank each day is approximately normal with mean 478 transactions and standard deviation 64 transactions. Which of the following is closest to the proportion of daily transactions greater than 350 ?

Answer 1

E) 0.977

Step-by-step explanation:

From the question we have that the mean number of transactions is 478 and standard deviation is 64.

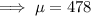`\implies \mu=478` and
`\sigma=478`

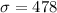
We want to find the proportion of daily transaction that is greater than 350 i.e
`P(X\:>\:350)`

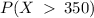
We first find the z-score using the formula:

`Z=(x-\mu)/(\sigma)`

`Z=(350-478)/(64)=-2`

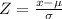
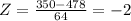
Reading from the standard normal distribution table
`P(X\:<\:350)=0.0228`

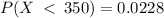
Note that:

`P(X\:>\:350)=1-P(X\:<\:350)`

`\implies P(X\:>\:350)=1-0.0228=0.9772`

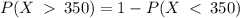
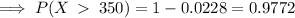
Therefore the proportion of daily transactions greater than 350 is 0.977

The last option is correct