Answer:
(³/₂, 5)
Explanation:
The limitation that x ≥ 0 and y ≥0 limits us to the first quadrant.
1. Plot the two inequalities
See the diagram below.
The graph of y ≤ ⅔x + 4 is represented by the red line and the red area below it.
The graph of 8 ≥ y + 2x is represented by the blue line and the blue area below it.
The purple area is the region in which all conditions are satisfied.
2. Determine the point at which the two lines intersect
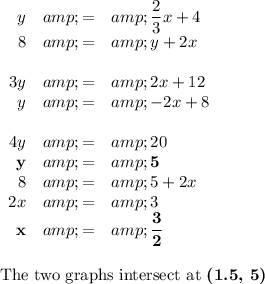
3. Determine the equation for D
The line should include the point (1.5, 5)
D = 6x -3y = 6×1.5 - 3×5 = 9 - 15 = -6
The equation of the objective function is
6x - 3y = -6
It is represented by the black line in the diagram and its maximum occurs at
(³/₂, 5)