The speed of the planes are 300 miles per hour and 355 miles per hour.
Solution:
Given, Two planes are 1965 miles apart, flying toward each other.
Their speeds differ by 55 mph.
They pass each other in 3 hours,
We have to find what is the speed of each?
Let the speed of 1st plane be s miles per hour, then speed of the other plane will be s + 55 miles per hour.
And, distance travelled by 1st plane be d, then distance travelled by other plane will be 1965 – d miles
Now, we know that, distance = speed
 time
time
So, for 1st plane ⇒
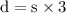
For 2nd plane ⇒
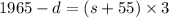
By using 1st plane equation
1965 – 3s = 3s + 165
1965 – 165 = 3s + 3s
6s = 1800
s = 300
So, speed of 1st plane is 300 miles per hour, then speed of 2nd plane will be 300 + 55 = 355 miles per hour.
Hence, the speed of the planes are 300 miles per hour and 355 miles per hour.