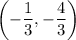Question

Anyone know what the vertex would be ?

Answer 1

`\left(-(1)/(3),-(4)/(3)\right)`

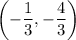
Explanation:

The graph of the parabola passes through the points (-1,0), (0,-1) and (1,4).

Let
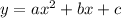`y=ax^2+bx+c` be the equation of the parabola. Substitute the coordinates of the points:

`0=a\cdot (-1)^2+b\cdot (-1)+c\Rightarrow a-b+c=0\\ \\-1=a\cdot 0^2+b\cdot 0+c\Rightarrow c=-1\\ \\4=a\cdot 1^2+b\cdot 1+c\Rightarrow a+b+c=4`

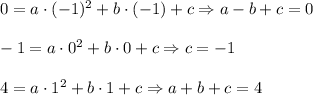
Substitute
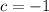`c=-1` into the first and third equations:

`a-b-1=0\Rightarrow a-b=1\\ \\a+b-1=4\Rightarrow a+b=5`

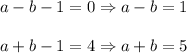
Add them:

`a-b+a+b=1+5\\ \\2a=6\\ \\a=3\\ \\3-b=1\\ \\b=3-1=2`

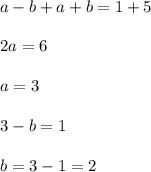
Hence,

`y=3x^2+2x-1`

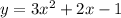
Find the vertex:

`x_v=(-b)/(2a)=(-2)/(2\cdot 3)=-(1)/(3)\\ \\y_v=3\cdot \left(-(1)/(3)\right)^2+2\cdot \left(-(1)/(3)\right)-1=(1)/(3)-(2)/(3)-1=-(4)/(3)`

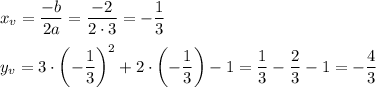
So, the vertex has coordinates

`\left(-(1)/(3),-(4)/(3)\right)`