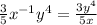Answer:
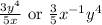
Explanation:
The expression is:

First, we will multiply the numerators together and denominators together.
This gives,
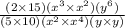
Now, we use the exponent property
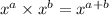 .
.
This gives,
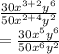
Now, we use the exponent property

This gives,
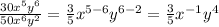
From the properties of exponents,
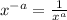
So,