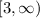Question

Graph the function f(x)=|x|+3 .State the domain and range .​

Answer 1

Domain is all real numbers. Range is
`[3,\infty)`

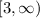
Explanation:

The function
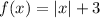`f(x)=|x|+3` is a transformation of the parent function
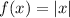`f(x)=|x|` by moving the function up by 3 units.

So, the graph of the function is shown below.

From the graph, it is clear that the
`x` values has no limitation and hence can take any real values. Domain is the set of all possible
`x` values.

So, domain is the set of all real numbers.

Range is the set of all possible values for
`y` for the given domain.

From the graph, the minimum value of
`y` is at the point (
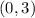`(0,3)`. So, the minimum value of y is 3. The
`y` value then goes on increasing towards infinity.

Therefore, range is a real number greater than or equal to 3.

So, range is
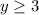`y\geq 3` or
`[3,\infty)`