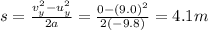Question

A rubber band projectile was launched by Cody at an angle of 500 from the

floor, while Aaron took the time. It took the rubber band 1.60 seconds to
land on the other side of the dome. The horizontal distance that was
measured by Samantha was 12 meters. Calculate the initial velocity of the
rubber band and its highest point from the floor.

Answer 1

1) Initial velocity: 11.7 m/s

The motion of the rubber band is a projectile motion, so it has:

- A uniform motion along the horizontal direction

- A free-fall motion along the vertical direction

Since the motion along the horizontal direction is uniform, the horizontal velocity is constant, and it can be calculated as:

`v_x = (d)/(t)`

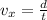
where

d = 12 m is the horizontal distance travelled

t = 1.60 s is the total time of flight

Substituting,

`v_x = (12)/(1.60)=7.5 m/s`

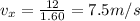
We also know that the horizontal velocity is related to the initial velocity of the projectile by

`v_x = u cos \theta`

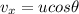
where

`\theta=50^(\circ)` is the angle of projection

u is the initial velocity

Solving for u,

`u=(v_x)/(cos \theta)=(7.5)/(cos 50)=11.7 m/s`

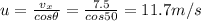
2) Highest point: 4.1 m

The initial velocity along the vertical direction is:

`u_y = u sin \theta = (11.7)(sin 50)=9.0 m/s`

The motion along the vertical direction is a free fall motion, so we can use the following suvat equation

`v_y^2 - u_y^2 = 2as`

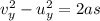
where

`v_y` is the vertical velocity after the projectile has covered a vertical displacement of s

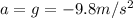`a=g=-9.8 m/s^2` is the acceleration of gravity

At the point of maximum height, the vertical velocity is zero:

`v_y=0`

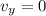
So, if we substitute it into the equation, we can find s, the maximum height:

`s=(v_y^2-u_y^2)/(2a)=(0-(9.0)^2)/(2(-9.8))=4.1 m`