Answer:
The roots of the polynomial equation x^3 - 7x = 6x - 12 is 1, 3, -4 Hence option B is correct
Solution:
Given that the polynomial equation is

We are asked to find the roots of the polynomial


On solving we get,
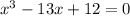
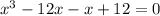
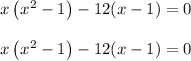
(x-1)(x(x+1)-12)=0
(x-1)(x-3)(x+4)=0
x = 1, 3, -4
Hence the roots of the polynomial equation x^3 - 7x = 6x - 12 is 1, 3, -4 Hence option B is correct