Question

A soccer ball rolls to a stop of 21 m/s with a deceleration of -2.0 m/s. How far does it roll until it stops?

Answer 1

The distance covered by the soccer ball before coming to rest is calculated as 110.25 m.

Step-by-step explanation:

As the ball rolls to a stop from the initial velocity of 21 m/s and it is said to exhibit the deceleration of -2.0 m/s. As the time taken to stop the ball has not been given, then the distance covered by the ball before stopping can be determined by using the third equation of motion. So, according to this,

`2 a s=v^(2)-u^(2)`

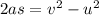
Thus, rearranging the equation, we get as follows,

`s=(v^(2)-u^(2))/(2 a)`

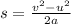
So, the distance up to which the ball rolled before stopping is s.

`s=((0)^(2)-(21)^(2))/(-2 * 2)=(-441)/(-4)=110.25`

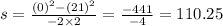
Hence, the soccer ball travelled 110.25 m far until it stops.

Answer 2

Answer:110.25 m

Explanation:v^2 = u^2 + 2as

21^2 = 0 - 2*2*s

s = 441/4

s=110.25 m