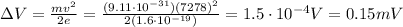Question

Through what potential difference must electrons be accelerated so that they will exhibit wave nature in passing through a pinhole 0.10 micrometers in diameter?​

Answer 1

0.15 mV

Step-by-step explanation:

In order to exhibit wave nature, the de Broglie wavelength of the electron must be of the same size of the diameter of the pinhole, therefore:

`\lambda=0.10 \mu m = 1.0\cdot 10^(-7) m`

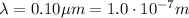
The de Broglie wavelength of an electron is

`\lambda = (h)/(mv)`

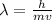
where

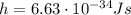`h=6.63\cdot 10^(-34) Js` is the Planck constant

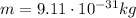`m=9.11\cdot 10^(-31) kg` is the mass of the electron

v is the electron's speed

Therefore, the electron's speed must be

`v=(h)/(m\lambda)=(6.63\cdot 10^(-34))/((9.11\cdot 10^(-31))(1.0\cdot 10^(-7)))=7278 m/s`

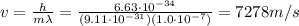
When accelerated through a potential difference
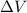`\Delta V`, the kinetic energy gained by the electron is equal to the change in electric potential energy, therefore

`e\Delta V = (1)/(2)mv^2`

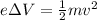
where

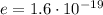`e=1.6\cdot 10^(-19)` is the magnitude of the charge of the electron

So, we can find the potential difference needed:

`\Delta V=(mv^2)/(2e)=((9.11\cdot 10^(-31))(7278)^2)/(2(1.6\cdot 10^(-19)))=1.5\cdot 10^(-4)V = 0.15 mV`