Question

True or false. If two numbers are relatively prime, both numbers are prime. Give an example!!!! Please help ASAP!!! :(

Answer 1

It's false. Two numbers are relatively prime if they have no common divisors. Of course two (different) primes will surely be relatively prime, but you can easily build two composite relatively prime numbers.

For example, let's build a number using only the primes 2 and 3:

`n = 2^3\cdot 3^2=72`

and another one using only the primes 5 and 7:

`m = 5\cdot 7^3=1715`

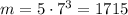
these numbers are relatively prime, because they share no common divisors (because no primes appear in both factorizations), but none of them is prime.

Answer 2

• FALSE
• 8, 9 are relatively prime; neither is prime

Explanation:

"Relatively prime" simply means the numbers have no common factors. That does not mean that the numbers do not have more than one factor.

8 = 2·2·2

9 = 3·3

have no common factors, so are relatively prime. Neither is a prime number, as each has multiple prime factors.

__

The factors need not be repeated. The following numbers are all relatively prime:

4 = 2·2

5 = (prime)

21 = 3·7

143 = 11·13