Question

The perimeter of a rectangular garden is 196 meters. The width of the garden is 34 meters less than the length. Find the length and the width.

Answer 1

Plz. Look for picture below

Answer 2

Length L = 66 meters

Width W = 32 meters

Explanation:

A rectangle is a figure of 4 sides, with two parallel sides each measuring what we call the width (W), and the other two measuring each what we call the length (L). Therefore the rectangle's perimeter (P) is the addition of these four sides (two widths and two lengths) which should equal 196 meters:
`P=W+W+L+L \\P = 2*W+2*L`

`196=2*W+2*L`

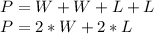
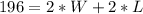
We can also write another equation with the information about the relationship between the rectangle's length (L) and its width (W): "The width of the garden is 34 meters less than the length."

This in mathematical form can be written as:
`W=L-34`

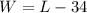
We can use this last equation to replace W in terms of L in the first equation above:

`196=2*W+2*L\\196=2*(L-34)+2*L\\196=2*L-2*34+2*L\\196=4*L-68\\196+68=4*L\\264=4*L\\L=(264)/(4) \\L=66`

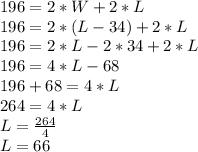
Therefore L = 66 meters

Now with this info we can find the value of the width (w) by replacing L with 66 in the second equation we found above:

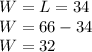`W=L=34\\W=66-34\\W=32` That is: the rectangle's width is 32 meters.