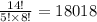Answer:
18018
Explanation:
Given:
Number of cans = 14
Number of cans of corn = 5
Number of cans of olives = 1
Number of cans of beans = 8
When there are
 objects to be arranged in order, out of which
objects to be arranged in order, out of which
 objects are of one kind,
objects are of one kind,
 objects are of another and so on, then the number of different arrangements is given as:
objects are of another and so on, then the number of different arrangements is given as:

Here,
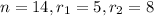
Therefore, the distinct orders in which the cans can be arranged is