Answer:
68.27%
Explanation:
An empirical rule for a normal distribution states that 68.27% of data is within 1 standard deviation (
 ) of the mean (
) of the mean (
 ), 95.45% of the data is within 2 standard deviations of the mean, and 99.73% of the data is within 3 standard deviations of the mean.
), 95.45% of the data is within 2 standard deviations of the mean, and 99.73% of the data is within 3 standard deviations of the mean.
The problem asks for the probability that a battery will last between 6.8 and 9.2 hours considering that
 =8 and
=8 and
 =1.2.
=1.2.
So, if the distribution is normal, the 68.27% of data is within 1
 , that is between
, that is between
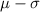 and
and
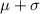 , replacing the values we have
, replacing the values we have
8-1.2=6.8 and 8+1.2=9.2
So, 68.27% of batteries will last between 6.8 and 9.2 hours