Question

Problem 5 A block of mass 3 kg slides on a horizontal, rough surface towards a spring with k = 500 N/m. The kinetic friction coefficient between the block and the surface is µk = 0.6. If the block’s speed is 5 m/s at the instant it first makes contact with the spring, (a) Find the maximum compression of the spring. (b) Draw work-energy bar diagrams for the process of the block coming to a halt, taking the system to be the block and the surface only

Answer 1

Step-by-step explanation:

Given that,

Mass of block = 3 kg

Spring constant k=500 N/m

Friction coefficient = 0.6

Speed = 5 m/s

(a). We need to calculate the maximum compression of the spring

Using work energy theorem

`(1)/(2)mv^2+\mu* mgx=(1)/(2)kx^2`

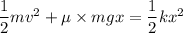
Put the value into the formula

`(1)/(2)*3*(5)^2+0.6*3*9.8* x=(1)/(2)*500* x^2`

`250x^2-17.64x-37.5=0`

`x=-0.354\ m`

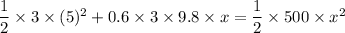
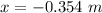
Negative sign shows the compression.

The maximum compression of the spring is 0.354 m.

(b). We need to draw the bar diagram

We need to calculate the initial energy

`E_(i)=(1)/(2)kx^2`

Put the value into the formula

`E_(i)=(1)/(2)*500*(0.354)^2`

`E_(i)=31.329\ J`

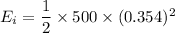
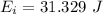
We need to calculate the final energy

Using formula of final energy

`E_(f)=(1)/(2)mv^2`

`E_(f)=(1)/(2)*3*(5)^2`

`E_(f)=37.5\ J`

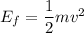
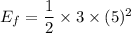
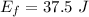
We need to calculate the work

Using formula of work

`W=Fx`

`W=\mu mg* x`

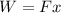
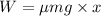
Put the value into the formula

`W=0.6*3*9.8*(-0.354)`

`W=-6.244\ J`

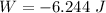
Hence, This is the required solution.

Answer 2

Step-by-step explanation:

given,

mass of block = 3 kg

spring constant k = 500 N/m

kinetic friction coefficient µk = 0.6

speed of block = 5 m/s

F = µk N

F = 0.6 x 3 x 9.8

F = 17.64 N

using energy conservation

`(1)/(2)mv^2=(1)/(2)kx^2+Fx`

`(1)/(2)* 3 * 5^2=(1)/(2)* 500 * x^2+17.64* x`

250 x² + 17.64 x - 37.5 = 0

on solving

x = 0.354 m

graph is attached below