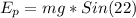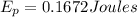Question

Find the absolute value of the change of the gravitational potential energy (GPE) of the puck-Earth system from the moment the puck begins to move to the moment it hits the spring. Use 0.253 m for the displacement of the puck along the ramp and 9.80 m/s2 for the acceleration due to gravity. Assume that the mass of the puck is 0.180 kg.

Answer 1

GPE=0.4462J

Step-by-step explanation:

Given Data

h=0.253m

g=9.80m/s²

m=0.180kg

To find

Gravitational potential energy (GPE)

Solution

GPE=mgh

where

• m is mass

• h is height

• g is gravity

GPE=mgh

GPE=(0.180kg)×(9.8m/s²)×(0.253m)

GPE=0.4462J

Answer 2

0.1672 Joules

Step-by-step explanation:

The gravitational potential energy is given by the following formula

`E_ {p} = mgh`

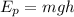
Where,

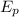`E_ {p}` = = Potential energy

m = mass

g = Gravitational Field Strength

h = Vertical Height

Since the launch is made at an angle of inclination,

our objective of interest is the vertical component of that angle,

that is Sin (\ theta)

Where the angle is

`\theta = 22^(\circ)`

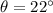
In this way,

`E_ {p} = mg * Sin (22)`

`E_ {p} = 0.18 * 9.8 * 0.253 * Sin (22)`

`E_ {p} = 0.1672 Joules`