Question

The 100-lb block slides down the inclined plane for which the coefficient of kinetic friction is 0.25 k = . It is moving at 10ft/s when it reaches the point A, 10ft from B along the inclined plane.

Find a) (2pt) the change in Potential energy of the block going from A to B.

b) (3pt) the work done against friction going from A to B, and the speed of the block at B.

c) (5pt) the maximum deformation of the spring  needed to momentarily arrest (stop) the motion of the block

Answer 1

Given data in the problem statement

weight of block=100 lb

velocity=10 ft/s

height=10 ft

Potential energy=m*g*h

Potential energy=100*9.8*10=9800 lb

Answer 2

Once the force diagram has been made, we proceed to determine the variables we have,

So

The weight of the block (W)

`W = 100lb`

Friction coefficient

`\mu = 0.25`

Block speed,

`v = 10ft / s`

For the balance of forces we perform summation, as well,

`\sum F_y = 0 \Rightarrow N-Wsin \theta = 0`

`sin \theta = \frac {4} {\sqrt {4 ^ 2 + 3 ^ 2}} = 0.8 \Rightarrow \theta = 53.14 ^ {\circ}`

`N = (100) * sin (53.13) = 80lb`

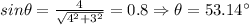
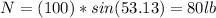
We can proceed to solve the energy equation as well

`V + T = W_ {1-2}`

`\frac {1} {2} \frac {W} {g} v ^ 2- \mu N (10 + x) - \frac {1} {2} kx ^ 2 = -Wcos \theta (10 + x)`

`\frac {1} {2} \frac {100} {32.2} 10 ^ 2 - (0.25) (80) (10 + x) - \frac {1} {2} (200) x ^ 2 = -100cos ( 53-13) (10 + x)`

`100x ^ 2-40x-555.28 = 0`

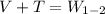
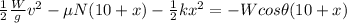
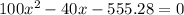
Solving the equation for 0, we find that the maximum deflection is x = 2.5ft