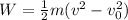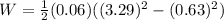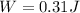Answer with Explanation:
We are given that mass of block=0.0600 kg
Initial speed of block=0.63 m/s
Distance of block from the hole when the block is revolved=0.47 m
Final speed=3.29 m/s
Distance of block from the hole when the block is revolved=

a.We have to find the tension in the cord in the original situation when the block has speed =
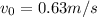
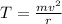
Because tension is equal to centripetal force
Substitute the values
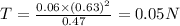
b.
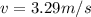
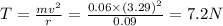
c.Work don=Final K.E-Initial K.E