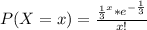Question

Nico met Claire Boucher (Grimes) at McGill. He has been waiting for the release of her next album. Assume that the waiting time is exponential with mean 3 years. To keep up with releases Nico receives Resident Advisor’s monthly album review newsletter. Assume that the album will be featured in the next issue after its release. Let X be the number of newsletters required to get news of the release of the album. Find the probability mass function of X

Answer 1

`P(X=x)=\frac{(1)/(3)^(x)*e^{-(1)/(3)} }{x!}`

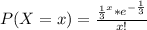
Explanation:

According to the probabilistic relationship between the exponential distribution and the Poisson distribution, which expresses that if the time between events is exponential with mean m (rate L=1/m) then the number of events of a t time is Poisson with a L*t parameter. Therefore, the probability mass function is given by,

`P(X=x)=(L^(x)*e^(-L) )/(x!)`

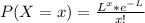
Where,

`L=(1)/(m)`

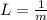
m: mean

In this case as we have that the mean is 3 (that is m=3), then the probability mass function of X is:

`P(X=x)=\frac{(1)/(3)^(x)*e^{-(1)/(3)} }{x!}`