Question

A 5.0 kg box is sliding across a waxed floor by the application of a 15 N east force. If the force of friction is 2.5 N west, what is the net force acting on the box? Whis is the box's acceleration

Answer 1

1) 12.5 N east

There are two forces acting on the box along the horizontal direction:

- The applied force of 15 N east, we indicate it with F

- The force of friction of 2.5 N west, we indicate it with
`F_f`

Taking east as positive direction, we can write the two forces has

`F=+15 N\\F_f = -2.5 N`

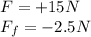
Therefore, the net force on the box will be:

`F_(net) = F + F_f = 15 + (-2.5) = +12.5 N`

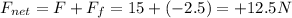
And the positive sign means the direction is east.

2)
`2.5 m/s^2`

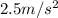
We can solve this part by using Newton's second law:

`F_(net)=ma`

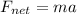
where

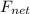`F_(net)` is the net force on the box

m is its mass

a is the acceleration

For the box in this problem,

`F_(net) = 12.5 m/s^2` (east)

m = 5.0 kg

Solving for a, we find the acceleration:

`a=(F_(net))/(m)=(12.5)/(5.0)=2.5 m/s^2`

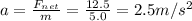
And the direction is the same as the net force (east)