Question

A uniform stick 1.5 m long with a total mass of 300 g is pivoted at its center. A 3.0-g bullet is shot through the stick midway between the pivot and one end The bullet approaches at 250 m/s and leaves at 140 m/s.

With what angular speed is the stick spinning after the collision?
ω= rad/s

Answer 1

given,

length of stick = 1.5 m

mass of the stick = 300 g = 0.3 kg

mass of bullet, m = 3 g = 0.003 kg

initial velocity (v_1) = 250 m/s

final velocity (v_2) = 150 m/s

distance of the pivot point from center

`r = (H)/(4)`

`r = (1.5)/(4)`

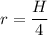
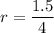
r = 0.375 m

angular momentum of stick after collision

`L_(stick) = L_i - L_f`

=
`mv_ir - mv_fr`

=
`mr(v_i-v_f)`

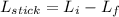
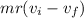
= 0.003\times 0.375 \times (250-140)[/tex]

= 0.12375 kg.m²/s

momentum of inertia

`I = (1)/(12)MH^2`

`I = (1)/(12)* 0.3 * 1.5^2`

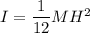
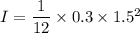
angular speed of stick

`\omega_(stick)= (L_(stick))/(I)`

=
`(0.12375)/(0.05625)`

= 2.2 rad/s

Answer 2

Answer:2.2 rad/s

Step-by-step explanation:

Given

Length of stick=1.5 m

mass m=300 gm

mass of bullet
`m_0=3 gm`

approach velocity of bullet=250 m/s

Final Velocity of Velocity=140 m/s

Distance of Pivot to bullet hit is
`r=(L)/(4)=0.375 m`

Conserving Angular Momentum

Initial momentum
`L_i=mv_i\cdot r`

`L_i=3* 10^(-3)* 250* 0.375=0.281 kg.m^2/s`

`L_f=mv_f\cdot r`

`L_f=3* 10^(-3)* 140* 0.375=0.157 kg.m^2/s`

Moment of inertia of rod about Pivot
`=(mL^2)/(12)=0.05625 kg.m^2`

`L_(net)=I* \omega _(stick)`

`0.281-0.157=0.05625* \omega _(stick)`

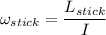
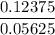
`\omega _(stick)=(0.124)/(0.05625)=2.2 rad/s`