Question

The demand function for a product is p=30−3q where p is the price in dollars when q units are demanded. Find the level of production that maximizes the total revenue and determine the revenue. A) Q= units

B) R= $

Answer 1

A) Quantity, q = 5 units.

B) Revenue, r = $75.

Explanation:

The demand function for a product is

`p=30-3q`

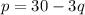
where p is the price in dollars when q units are demanded.

Revenue = Price × Quantity

Using the given information, the revenue function is

`R=p* q`

`R=(30-3q)* q`

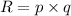
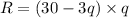
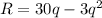`R=30q-3q^2` .... (1)

Differentiate with respect to q.

`(dR)/(dq)=30(1)-3(2q)`

`(dR)/(dq)=30-6q`

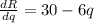
Equate
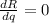`(dR)/(dq)=0` to find the critical value of q.

`30-6q=0`

`30=6q`

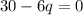
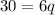
Divide both sides by q.

`5=q`

The value of q is 5.

Differentiate
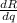`(dR)/(dq)` with respect to q.

`(d^2R)/(dq^2)=-6>0`

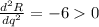
So, the revenue function is maximum at q=5.

Substitute q=5 in equation (1).

`R=30(5)-3(5)^2`

`R=150-75`

`R=75`

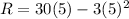
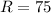
Therefore, the level of production that maximizes the total revenue is 5 units and the revenue is $75.

Answer 2

Answer: a) Q= 5units

b) R= $75

Explanation:

The maximum revenue is at dR/dq = 0

Revenue = price x quantity of demand = p × q

Substituting p = 30- 3q

R = (30-3q) × q

R= 30q- 3q2 (q2 = q raised to the power of 2)

dR/dq = 30- 6q = 0

6q = 30

q= 30/6= 5

q= 5 units

R = pq= 30q- 3q2

R= 30(5) - 3( 5×5)

R= 150- 75

R= $75

Goodluck...