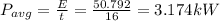Answer:
Step-by-step explanation:
Given
mass of wheel m=13 kg
radius of wheel=1.8 m
N=469 rev/min
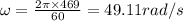
t=16 s
Angular deceleration in 16 s

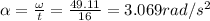
Moment of Inertia

Change in kinetic energy =Work done
Change in kinetic Energy
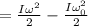
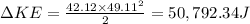
(a)Work done =50.79 kJ
(b)Average Power