Question

In a manufacturing facility, 2-in-diameter brass balls (k = 64.1 Btu/h· ft·°F, rho = 532 lbm/ft3 , and cp = 0.092 Btu/lbm·°F) initially at 250°F are quenched in a water bath at 120°F for a period of 2 min at a rate of 120 balls per minute . If the convection heat transfer coefficient is 42 Btu/h·ft2 ·F, determine

(a) the temperature of the balls after quenching and (b) the rate at which heat needs to be removed from the water in order to keep its temperature constant at 120°F.

Answer 1

A) T(t) = 166 degree F

B) Q total = 1196 Btu/min

Step-by-step explanation:

check for characteristics length and Biot number

`Lc = (V)/(A_s) = ((\pi D^3)/(6))/(\pi D^2) = ( D)/(6)`
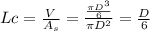
`Lc = ((2)/(12) ft)/(6) = 0.02778 ft</p><p></p><p>[tex]Bi = (hL)/(k) = (42 * 0.02778)/(64.1) = 0.01820 <0.1`

As Biot number is less than 0.1 so it can be determined as lumped parameter system

A) we know that

`b =  (42)/(532 * 0.092 * 0.02778) = 30.9 h^(-1)`

`(T(t) - T_(\infity))/(T_i -T_(\infity)) = e^(-bt)`

`(T(t) - 120)/(250 -120) = e^(-0.00858* 120)`

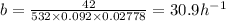
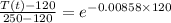
solving for T(t) we get

T(t) = 166 degree F

b) we know that

`m  = \rho V =  \rho* (\piD^3)/(6)`

`m = 532 * (\pi (2/12)^3)/(6) = 1.290 lbm`

`Q = mCp (T_2 - T(t))`

`Q = 1.29 * 0.092 (250 - 166) = 9.97 Btu`

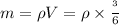
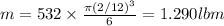
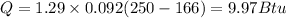
Heat removed from water

`Q total = n_(ball) * Q_(ball)`

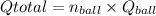
= (120 balls/min)×(9.97 Btu)

Q total = 1196 Btu/min