Question

Use an equation to find the value of k so that the line that passes through the given slope (1,3) , (5,k) m=2

Answer 1

The value of k with given points and slop = 11

Explanation:

Given that a line passes through two points having slop (m) = 2

co ordinates of points are (1 , 3) and (5 , k)

Now slop of line can be written as,

Slop =
`((y2 - y1))/((x2 - x1))`

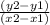
Or, m =
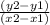
`((y2 - y1))/((x2 - x1))`

2 =
`((k - 3))/((5 - 1))`

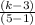
Or, 2 =
`((k - 3))/((4))`

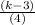
So , k - 3 = 8

∴ K = 8+3 = 11

Hence the value of k with given points and slop = 11 Answer