Answer:
1. Plot the point (–2,4).
2. From that point, count left 3 units and down 1 unit and plot a second point.
3. Draw a line through the two points.
Explanation:
Given:
The equation is:
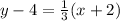
Express this in the standard form,

Where,
 is the slope of the line and
is the slope of the line and
 is the y-intercept.
is the y-intercept.
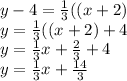
So, the slope is
 and y-intercept is
and y-intercept is
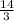 .
.
Now, for
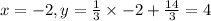
So, first we plot the point
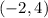 .
.
Since, the slope is
 , we have to move 3 units to left and then 1 unit down to plot a second point.
, we have to move 3 units to left and then 1 unit down to plot a second point.
Slope is positive, therefore, we have to move left and then down
Lastly, we have to draw a line passing through these two points to graph the equation
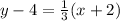 .
.