Question

Given: The sun is 1.5 × 108 km from Earth. The index of refraction for water is 1.297. How much longer would it take light from the sun to reach Earth if the space between them were filled with water rather than a vacuum? 1. 3.13551 2. 2.47672 3. 3.07713 4. 2.29326 5. 2.35163 6. 2.20153 7. 3.01042 8. 2.52675 9. 2.25156 10. 2.85198 Answer in units of min.

Answer 1

option (2) 2.47672

Step-by-step explanation:

Data provided in the question:

Distance between the sun and the Earth = 1.5 × 10⁸ km = 1.5 × 10¹¹ m

The index of refraction for water = 1.2973

Now,

Speed of light in water, v =
`\frac{\textup{Speed of light in vacuum}}{\textup{Refractive index of water}}`

also,

speed of light in vacuum = 3 × 10⁸ m/s

thus,

Speed of light in water, v =
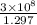`\frac{3*10^8}{\textup{1.297}}` m/s

now,

if the space between the sun and the Earth is filled with water, time (t) taken by the light to reach Earth from sun will be

Time =
`\frac{\textup{Distance between the Sun and the Earth}}{\textup{Speed of light in Water}}`

or

Time =
`\frac{1.5*10^(11)}{\frac{3*10^8}{\textup{1.297}}}`

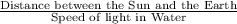
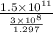
or

Time = 648.5 seconds

Time taken by light to reach Earth in vacuum

=
`\frac{\textup{Distance between the Sun and the Earth}}{\textup{Speed of light in Vacuum}}`

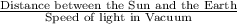
or

Time =
`(1.5*10^(11))/(3*10^8)`

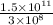
or

Time = 500 seconds

Therefore,

the difference in time = 648.5 - 500 = 148.5 seconds

or

=
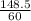`\frac{\textup{148.5}}{\textup{60}}` minutes

= 2.475 minutes ≈ 2.47672

Hence, the correct answer is option (2) 2.47672