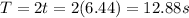Question

A ball is projected 203 meters straight upward and then falls the same distance back to its starting point.

Neglecting air resistance, its total time in the air is about.​

Answer 1

12.88 s

Step-by-step explanation:

We can solve this problem by considering only the first half the motion, from the moment the ball is projected upward to the moment it reaches its maximum height.

Since this is a uniformly accelerated motion, we can use the following suvat equation:

`s=vt-(1)/(2)at^2`

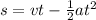
where:

s is the vertical displacement

v is the final velocity

t is the time

a is the acceleration

Here we have:

v = 0: the vertical velocity is zero when the ball has reached its maximum height, that is

s = 203 m

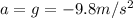`a=g=-9.8 m/s^2` (acceleration of gravity, negative because it is downward)

Solving the equation for t, we find the time at which the ball reaches the maximum height:

`t=\sqrt{-(2s)/(a)}=\sqrt{-(2(203))/(-9.8)}=6.44 s`

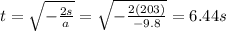
The second half of the motion is symmetrical and identical to the first one, so the total time in air is just twice this time, therefore:

`T=2t=2(6.44)=12.88 s`