Question

You decide to put $2,000 in a savings account to save for a $3,000 downpayment on a new car. If the account has an interest rate of 4% per year and is compounded monthly

how long does it take until you have $3.000 without depositing any additional funds?
121.862 years
1
12.1862 years
|
10.155 years
1.0155 years

Answer 1

1.0155 years is the correct answer

Answer 2

`t \approx 10.15351... \ (years)`

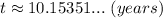
Explanation:

Interest compound is defined as

`A=P(1+(r)/(n))^(nt)`

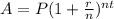
Where,

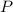`P` is the principal.

`r` is the rate in decimal.

`n` is the number of compounded periods within a year.

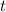`t` is the time in years.

In this case, we have

`P=2000\\A=3000\\r=4\%=0.04\\ n=12\\t=?`

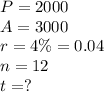
Replacing all values, we have

`3000=2000(1+(0.04)/(12))^(12t)`

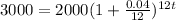
Now, we solve for
`t`

`(3000)/(2000)=(1+ 0.003)^(12t)`

`1.5=(1.003)^(12t)`

`ln(1.5)=ln((1.003)^(12t) )\\ln(1.5)=12t * ln(1.003)\\12t=(ln(1.5))/(ln(1.003)) \\12t=(0.4)/(0.003)\\ 12t=133.33\\t=(133.33)/(12)\\ t \approx 11.11`

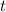
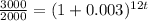
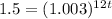
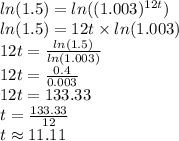
Our result is different because at each step we approximated results.

If you use a calculater, you would find a more exact result would be

`t \approx 10.15351...`

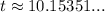
Therefore, the right answer is the third choice.