Question

A 50 kg block of ice slides down a frictionless incline 2.4 m along the diagonal and 0.54 m high. A worker pushes up against the ice, parallel to the incline, so that the block slides down at constant speed. (a) Find the magnitude of the worker's force. How much work is done on the block by (b) the worker's force, (c) the gravitational force on the block, (d) the normal force on the block from the surface of the incline, and (e) the net force on the block?

Answer 1

Step-by-step explanation:

Given that,

Mass of block = 50 kg

Friction less incline = 2.4 m

Diagonal height= 0.54 m

According to figure,

(a). We need to calculate the angle

Using formula of angle

`\sin\theta=(y)/(x)`

`\sin\theta=(0.54)/(2.4)`

`\sin\theta=0.225`

`\theta=\sin^(-1)(0.225)`

`\theta=13.00^(\circ)`

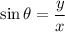
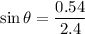
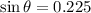
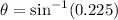
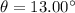
We need to calculate the force applied by the worker

Using formula of force

`F_(w)=mg\sin\theta`

`F_(w)=50*9.8*\sin13.00`

`F_(w)=110.2\ N`

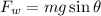
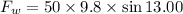
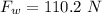
(b). We need to calculate the work done by the force applied by worker in opposite direction

Using formula of work done

`W=-F_(w)d`

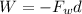
Put the value into the formula

`W=-110.2*2.4`

`W=-264.48\ J`

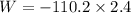
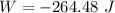
(c). We need to calculate the gravitational force

Using formula of gravitational force

`F_(g)=mg\sin\theta`

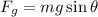
Put the value into the formula

`F_(g)=50*9.8*\sin13.00`

`F_(g)=110.2\ N`

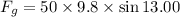
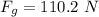
(d). We need to calculate the normal force on the block from the surface of the incline

The normal force acting on the block is perpendicular to distance traveled by the block.

So, the work done by the normal force is zero.

(e). We need to calculate the net force on the block

The block slides down with constant speed so the net force on the block is zero.

Hence, This is the required solution.