Answer:
The midpoint of the given segment is (-0.5, 3)
Explanation:
The formula for mid-point is
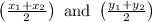
Now, from the given question endpoints A (-3,5) and B (2,1)
We know that
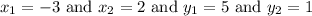
Substituting the values in the mid-point formula we get
x-coordinate is
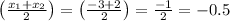
y-coordinate is
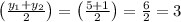
Hence, midpoint of the given endpoints is (-0.5,3) Thus we found the midpoint of the segment of the given end points.